a LaFrance Consulting Services™ publication
TwoOldGuys™ Study Guides
Plant Ecology Text
Chapter 9. Gradients
We have seen that the climatic regime to which plant communities must respond in order to persist
over the long-term. The climate is subject to several cycles;
a 10 - 12 year cycle (sunspot cycle),
an 80-year cycle (a putative cycle in sunspot cycle length),
a 950-year cycle (some data refer to this as a 510-year cycle, or a 750-year cycle [archeological data],
others describe a 1,500-year cycle; causes are unclear) plus
a 23,000-year cycle (Milankovitch cycle in precession of Earth's axis, pointing toward Polaris or Vega),
a 41,000-year cycle (Milankovitch cycle in Earth's axis tilt, 21.5° to 24.5°),
and a 100,000-year cycle (Milankovitch cycle in Earth's orbital eccentricity).
Classification:
Earlier (Chapter 2. “Life Zones & Biomes”) we saw classification at the Biome level.
Historically, Communities were classified before Biomes were. This was based on the ‘Community as
a super organism’ concept. The taxonomic units were named by the dominant plant(s), the physiognomy
(or general appearance of the Community, such as deciduous forest, coniferous forest, and desert scrub),
or by physical features (such as tidal flat, dune, pond, and stream). Note the similarity between this
classification and the Biome classification in Chapter 2:
| elevation |
Coves,
Canyons |
Draws,
Ravines |
Sheltered
slopes |
Open
slopes |
Ridges,
Peaks |
| 1800+ |
n/a |
n/a |
n/a |
n/a |
Heath
balds |
| 1600-1800 |
n/a |
Boreal Forest |
Grassy balds |
| 1300-1600 |
Beech,
mesic |
Beech,
sedge |
Hemlock |
Oak-
Chestnut |
| 1100-1300 |
Cove
forest |
Hemlock |
Oak-
Chestnut |
Pine
heath |
| 750-1100 |
Oak
forest |
Oak
heath |
Pitch
pine |
| 450-750 |
Oak-
Hickory |
Virginia
pine |
Ordination:
In the mid 20th Century we began developing more objective methods to
identify both the Communities and the environmental factors controlling them. At first, we ordered the
samples on the basis of a ‘similarity index.’ “In 1951, Curtis and McIntosh 1951
developed the ‘continuum index’, which later lead to conceptual links between species
responses to gradients and [to the use of] multivariate methods.” (downloaded 10 Mar 2011 from
ordination.okstate.edu/overview.htm). Then, “Bray and Curtis (1957) developed polar ordination,
which became the first widely-used ordination technique in ecology
(ordination.okstate.edu/overview.htm),” because it used geometric procedures [see ‘end
notes’ for this chapter below] to order the samples
between the two most dissimilar samples, making it easy to do without extensive calculations. Later,
multivariate statistical methods were tried as the (mainframe) computer became available to Ecologists.
[At my first teaching job (Indiana University Northwest), after administrative use of the computer (a
‘mini-mainframe’), one physics professor (high energy physics) used about half of the
faculty-available computer time (CPU seconds times memory), then I used about half of the remaining 50%
of total faculty-available computer time for Ecological analyses and simulations; the remaining 25% of
total faculty-available computer time was shared by the rest of the faculty.]
As it became “obvious” that the samples did not cluster (as communities) but formed a
nearly continuous curve in ‘Ordination space’, the ordered samples were called a continuum (a descriptive term for the nearly continuous change
in species composition between communities) [implying (or, better, concluding) that the species
of the Landscape were independently distributed].

gradient analysis:
The first of the gradient analysis studies, later called direct gradient analysis, selected sites
where several environmental factors vary along a geographic transect (usually mountainous regions,
where altitude can be used as a direct gradient index due to the large number of environmental
variables which correlate with altitude (soil particle size increases, preciptation increases,
temperature decreases, growing season shortens, …). The species responses (abundance or relative
abundance) are plotted on elevation, to determine the relationship between the species response
distributions and the covarying environmental factors. For the Grand Kankakee Marsh study, 2002 data,
the gradient index is distance from the ditch in meters (depth to perched water table gets deeper, soil
has greater sand and less organic material), the gradient is

Again, as more Ecologists began using computers, the idea of a synthetic gradient index based on
the covariance of environmental variables was developed. Then as the proponents of ordination realized
the potential of gradient analysis, indirect gradient analysis (ordering samples by similarity, and
&$8220mapping” (a topology concept) the environment on the continuum were sometimes used,
especially in areas where environmental factor covariance was weak. Many ordination studies
‘evolved’ to Gradient Analysis, although a few purely ordination studies still appear in the
literature occasionally.
We can also replot the data from the Grand Kankakee Marsh study (the direct gradient analysis
graph above) in the same style as we did in Chapter 6 (Competition & Niche) using simulated,
theoretical data, but this using time actual field data. Each species is added
‘on top’ of the already plotted species, to allow us to look in more detail at ‘resource
partitioning’ among species in the natural world.
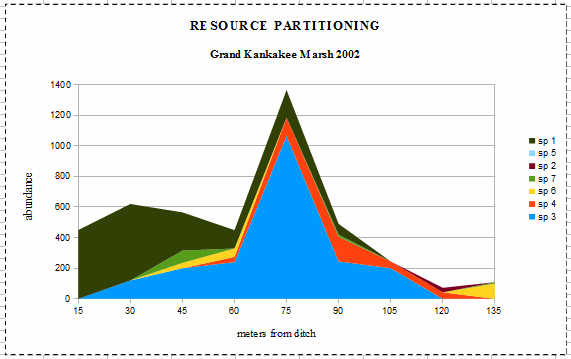
Species 1 (Sp 1) is an invasive species, Reed canarygrass (Phalaris arundinacea) which
“forms dense, highly productive single species stands that pose a major threat to many wetland
ecosystems. The species grows so vigorously that it is able to inhibit and eliminate competing
species” (downloaded 14 Mar 2011 from State of Washington,
Department of Ecology). At 15 meters from the ditch, it has formed a single-species stand. It had
a maximum population density at 30 meters and dropped off, becoming absent at 105 meters. The
‘resident naturalist’ told me that it had only invaded a few years earlier. It is possible
that the Reed canarygrass was responsible for the lack of significance between the species composition
and precipitation because its dynamics were strongly time dependent during the study [with maximum
population density at 60 meters in 2003, and at 60 - 75 meters in 2004 and extending across the entire
transect each year 2003 and 2004]. This illustrates well how invasive species tend to behave, at least
early during their invasion of new sites.
Species 3 (Sp 3) is a sedge (Carex bicknellii?) which is the ‘normal’ dominant in
wetlands of the Grand Kankakee Marsh. Curiously, its maximum population density is ‘too far’
from the ditch, and its curve is too narrow through what should be the optimal and suboptimal ranges.
This suggests that it has experienced niche compression (narrowing) as a result of competition from a
new invader, the Reed canarygrass.
Species 4 (Sp 4) is a water-tolerant grass (Big bluestem, Sorgastrum nutans). Its
distribution curve appears to be slightly a asymmetrical, suggesting competition with the sedge and
canarygrass on the side (of its distribution) closest to the ditch. The remaining 4 species (of the 7
most abundant species in the data set, as average of the three years) have very low populations
densities, suggesting that they are simply occupying what I called ‘unused resources’ earlier.
Species 7 (Sp 7) is another grass (switch grass?, Panicum vergatum which is usually a mesic
(neither too wet nor too dry, but “just right”) to dry-mesic species. In 2003, the driest of
the three years during the study, it experienced a large population increase at the dry end of the
transect, then returned to low population densities in 2004. Species 6 (Sp 6) is vetch (Vicia
villosa) is a woody legume which has ”escaped from cultivation” in Indiana [planted for
hillside stabilization and forage (University of Wisconsin-Madison, Cooperative Extension Service
pamphlet, downloaded 14 Mar 2011 from www.hort.purdue.edu], but growing readily in the wild, especially
on sandy, dry prairie sites. Species 5(Sp 5) is a introduced weedy species (chickweed, Stellaria
spp) of old fields (formerly cultivated) and pastures in Indiana. It was absent in 2002 & 2003, but
a clump of them was in the 90 meter sample, plus a few in each sample from 45 to 75 meters.
Using the third definition of carrying capacity (definition 3 in the glossary) as
“the capacity of the environment to support the populations of all species,
stated in terms of the sum of the populations of all species present,” and the theory of
Island Biogeography we can begin to see what the Theory of Plant Community Ecology will look like.
The populations of the first few species to immigrate to a new site, could each grow to its theoretical
maximum population density. Then, the ‘unused resources’ left over will be exploited by the
available species [according to the Illinois Natural History Survey, the biodiversity available is
wet-mesic prairie = 31 spp
dry-mesic upland forest = n/a
wet-mesic floodplain forest = n/a
wet floodplain forest = 117 spp
shrub swamps/marshes = variable biodiversity.
END NOTES
A technical discussion of modified Bray-Curtis ordination technique
Species abundances
in data set, 2002
| sp rank |
abundance, Ni |
| |
meters from ditch |
| 15 |
30 |
45 |
60 |
75 |
90 |
105 |
120 |
135 |
| 1 |
450 |
500 |
250 |
120 |
180 |
70 |
0 |
0 |
0 |
| 2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
30 |
0 |
| 3 |
0 |
120 |
200 |
240 |
1,065 |
245 |
200 |
0 |
0 |
| 4 |
0 |
0 |
0 |
34 |
120 |
160 |
44 |
42 |
0 |
| 5 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
| 6 |
0 |
0 |
35 |
55 |
0 |
0 |
0 |
0 |
100 |
| 7 |
0 |
0 |
80 |
0 |
0 |
15 |
0 |
0 |
0 |
To illustrate the ordination technique, we can look again at the Grand Kankakee Marsh study (Chapter
7). For simplicity, will we consider only the 7 most abundant species [3-year average], which account
for 94.35% of all individuals observed.
Conceptually, we can graph each species as a separate axis in an n-dimensional
space, where n is the number of species. Here n = 7, so we have a 7-dimensional space,
which is,admittedly, difficult to imagine. We need to reduce the number of dimensions to something
which is easier to imagine, usually 2-d (or sometimes 3-d [except these are difficult to draw on 2-d
paper]). Each sample (column) is plotted, as a vector in 7-d space with its origin at 0 and its point
at the point (n1, n2, n3,
n4, n5, n6,
n7); in this case (450, 0, 0, 0, 0, 0, 0), (500, 0, 120, 0, 0, 0, 0) …
. The distance from the origin of the graph is the square root of the sum of the abundances of
the 7 species (the scalar of the vector, for those of you who speak ‘mathematics’). More
‘interesting’ [see definition of interesting in the glossary]
is the distance between the vectors for the samples (also called “similarity between the
samples”), which is defined, in vector math, as the square root of the sum of the squares of the
differences between each of the 7 species. We should have to calculate the similarity between each of
the 81 possible differences between the 9 samples in our data set, and enter these differences into
a ‘similarity matrix.’ However, this matrix is symetrical - the similarity of sample 15 and
sample 30 is the same as the similarity between sample 30 and sample 15; and the similarity between
sample 15 and sample 15 is always zero, so we only have to calculate the remaining 36 similarities:
Similarity matrix
for data set, 2002
| |
15 |
30 |
45 |
60 |
75 |
90 |
105 |
120 |
135 |
|
X |
Y |
| 15 |
0 |
|
|
|
|
|
|
|
|
0 |
0 |
| 30 |
130 |
0 |
|
|
|
|
|
|
|
103 |
-132 |
| 45 |
296 |
277 |
0 |
|
|
|
|
|
|
262 |
138 |
| 60 |
413 |
404 |
163 |
0 |
|
|
|
|
|
604 |
420 |
| 75 |
1105 |
1005 |
880 |
238 |
0 |
|
|
|
|
1105 |
0 |
| 90 |
480 |
476 |
256 |
147 |
828 |
0 |
|
|
|
346 |
310 |
| 105 |
494 |
508 |
268 |
138 |
887 |
144 |
0 |
|
|
307 |
387 |
| 120 |
453 |
517 |
336 |
276 |
1083 |
283 |
202 |
0 |
|
115 |
389 |
| 135 |
461 |
524 |
334 |
274 |
1091 |
317 |
228 |
113 |
0 |
110 |
385 |
Once we have the similarity matrix, we locate the pair of samples with the highest dissimilarity,
in this case {15,75}. This line, 1105 units long, is the 1st axis in
ordination space. Using not particularly easy geometric equations, we can calculate (this is an algebra
problem, for those of you who “don't do algebra on Monday mornings&$8221) both the location of all
other samples on this axis, and the distance from the axis to each of them (both 15 and 75 are 0 units
from the line because we defined the line as passing through these two samples). One of these samples
will be the farthest from the line (in this case 105 meters, which is 387 units from the first axis).
The line perpendicular to the first axis and passing through sample 105 m is our second axis in
ordination space. Again with not particularly easy geometry equations (the good news is that the
algebra is identical to what we just did [but didn't show our work]), we can calculate the locations
of all samples on the 2ndaxis and their distance from the 2-d ordination
space (in case we want to do more algebra & geometry to get the 3rd
dimension in ordination space). In the past, we would calculate (pencil & paper, without the help
of computers, and even without calculators) all three dimensions, because we did not expect to get
curved lines in ordination space so tried to find the dimension in which the relationship is linear.
For theoretical reasons (the bell shaped species response curves), the relationship between samples
is curved. As a result, each extra dimension provides less new information (diminishing returns)
than the preceeding dimension. It is rarely worth the effort to calculate the
3rd dimension. For the field study I did to validate my first simulations
(LaFrance, Charles R. 1972. “Sampling and Ordination Characteristics of Computer-Simulated
Individualistic Communities.” Ecology 53:387–397.) [fortunately, I had access to a
mainframe computer to do the calculations using a FORTRAN program I wrote for the occasion], I had 120
species in about 200 samples [I could not use this data for the illustrations above because the field
data [as well as my FORTRAN programs] were on Hollerith (punch) cards which were damaged a few decades
ago].
RETURN to
ECOLOGY Outline
TwoOldGuys HOME
© 2010 TwoOldGuys ™
revised: 14 Mar 2011


